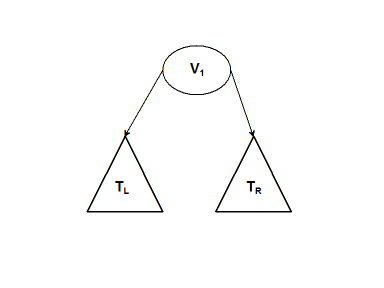
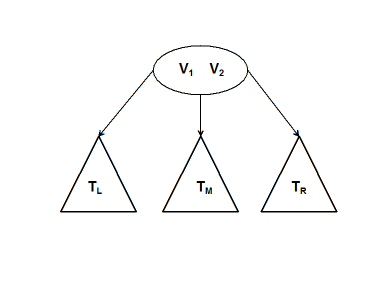
A 2-3 tree is a search tree that is always balanced. All insertions are made into leaf nodes and all leaves are at the same level.
In a BST, a node contains one value, its left child contains a value
less than the parent and its right child contains a value greater than the parent.
In a 2-3 tree there are two types of nodes: 2 nodes and 3 nodes:


A 2 node contains one value V1; all values in its left subtree are less than V1 and all values in its right subtree are greater than V1. A 3 node contains 2 values V1 and V2; all values in its left subtree are less than V1, all values in its middle subtree are greater than V1 and less than V2, and all values in its right subtree are greater than V1.
Insert a value v into a 2-3 tree:
When you split n and promote to its parent p, p may have one or two values already. If p has one value, the new value is added to p and the split ends. There are two cases, depending on whether n < p or p < n:
before split of n after
p n1 n1 p
/ \ / \ / | \
n x n2 n3 n2 n3 x
before split of n after
p n1 p n1
/ \ / \ / | \
x n n2 n3 x n2 n3
If the parent already has two values, then the parent must also be split. There are three cases for this split: n1 < p1 < p2, p1 < n1 < p2, and p1 < p2 < n1.
before split of n before split of p after
p1 p2 n1 n1 p1 p2 p1
/ | \ / \ / | | \ / \
n x1 x2 n2 n3 n2 n3 x1 x2 n1 p2
/ \ / \
n2 n3 x1 x2
before split of n before split of p after
p1 p2 n1 p1 n1 p2 n1
/ | \ / \ / | | \ / \
x1 n x2 n2 n3 x1 n2 n3 x2 p1 p2
/ \ / \
x1 n2 n3 x2
before split of n before split of p after
p1 p2 n1 p1 p2 n1 p2
/ | \ / \ / | | \ / \
x1 x2 n n2 n3 x1 x2 n2 n3 p1 n1
/ \ / \
x1 x2 n2 n3
Here is the pseudocode for the split:
split(n) {
if (n is the root)
create a new node p
else
let p be the parent of n
replace node n with two nodes n1 and n2, with p as their parent
give n1 the smallest item in n
give n2 the largest item in n
if (n is not a leaf) {
n1 is parent of n's two leftmost children
n2 is parent of n's two rightmost children
}
move the middle item in n up to p
if (p now has 3 items)
split(p)
}
Insert the numbers 5 25 10 40 50 20 75 15 45 60.
5 and 25 can both be placed in the same node. When 10 is inserted there is no room in the node so it is split and the middle value is promoted to the parent. When 40 is inserted there is room in the rightmost leaf.
5 5 25
10 10
/ \ / \
5 25 5 25 40
Now 50 should be inserted into the node with 25 and 40. Since this node already has two values, the node is split: 25 goes in the left child, 50 goes in the right child, and 40 gets promoted. Since 40 > 10, its left child (25) becomes the middle child, and its right child (50) becomes the right child. After that both 20 and 75 can be inserted into leaves.
10 40 10 40
/ | \ / | \
5 25 50 5 20 25 50
10 40
/ | \
5 20 25 50 75
Now 15 should be inserted into the node with 20 and 25. Since this node already has two values, the node is split: 15 goes in the left child, 25 goes in the right child, and 20 gets promoted. It would look like the following:
10 20 40
/ / \ \
5 15 25 50 75
But the parent already has two values, so it will be split: 10 goes in the right child, 40 goes in the right child, and 20 gets promoted to a new root. When 20 gets promoted its children get attached to 10 and 40 as shown in the final result below:
20
/ \
10 40
/ \ / \
5 15 25 50 75
Inserting 45 splits the node with 50 and 75, and 50 gets promoted to the parent:
20
/ \
10 40 50
/ \ / | \
5 15 25 45 75
Finally 60 is inserted and there is room in the rightmost leaf.
20
/ \
10 40 50
/ \ / | \
5 15 25 45 60 75
Email Me |
Office Hours |
My Home Page |
Department Home |
MCC Home Page
© Copyright Emmi Schatz 2016