| P |
Q |
F |
|---|---|---|
| 0 | 0 | A |
| 0 | 1 | B |
| 1 | 0 | C |
| 1 | 1 | D |
It is important to simplify a Boolean expression before using it to design a circuit, because a simpler expression will result in a simpler -- and thus faster and cheaper -- circuit. Simplifying expressions algebraically is difficult and one is not guaranteed to come up with a minimal expression.
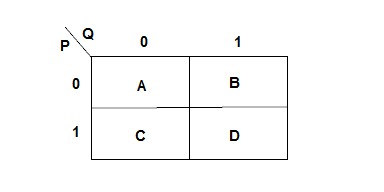
A Karnaugh map (or kmap) is a table which contains the information from a truth table, but in a different form.
The truth table for a function of two variables has four rows, so the kmap has four boxes.
|

|
The outer edges are labeled with the values of the input variables. Each cell in the map is the value of the function for the input values on the edges of that cell: put a 0 in the square if the function is 0 for that set of inputs, and put a 1 in the square if the function is 1 for that combination of inputs.
To use the Karnaugh map for simplifying, we group adjacent 1's in the body of the table. Each group is a block of two or four 1's. We must make the groups as large as possible and it's ok if they overlap -- i.e., a cell can be in more than one group. If a block which contains a 1 is not in any group, then it forms a group by itself. To simplify, look at each group and discard the variable that differs in the group.
|
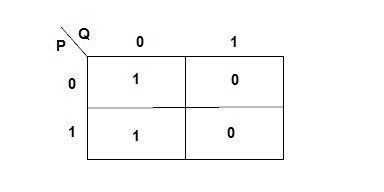
F = P Q + P Q = Q ( P + P) = Q |
The corresponding kmap is:
After grouping, we have:
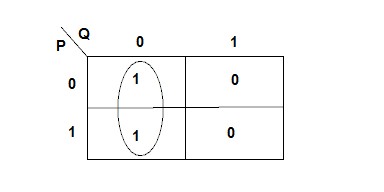
To simplify, we look at each group and discard the variable that differs in the group. In this example, our group has different values for P, but Q is always 0, so we discard P and get the expression Q. The reasoning for this is given above in the algebraic simplification of the function.
|
|
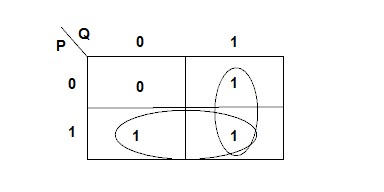
From the truth table we get:
F = P Q + P Q + P Q = P Q + P Q + P Q + P Q = Q (P + P) + P (Q + Q) = P + Q
From the kmap we get a term for each group (it has two overlapping groups). The "vertical" group differs in P so we get Q for that group. The "horizontal" group differs in Q so we get P for that group. The simplified expression is P + Q.
The truth table for a function of three variables has eight rows, so the kmap has eight boxes. For three variables we put one variable in the rows and two variables in the columns, so there are two rows and four columns. The column values are ordered differently than in the truth table. This is because we want neighboring column values to differ in only one of the variables.
The groups we form must contain either 2, 4, or 8 cells. We view the kmap now as a cylinder: a group can contain a cell or cells in the last column and the first column.
|
F = X Y Z + X Y Z + X Y Z |
The kmap for this function is:
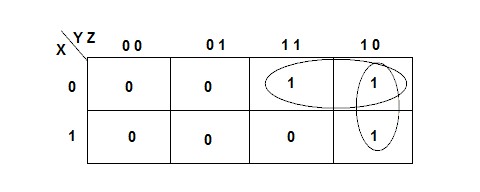
And the kmap gives us:
F = X Y + Y Z
|
F = X Y Z + X Y Z + X Y Z + X Y Z + X Y Z |
The kmap for this function is:
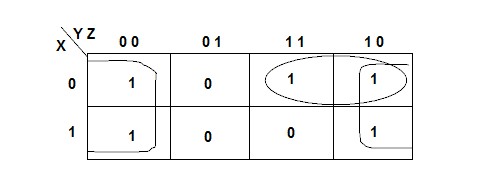
The kmap has two groups. One is the "horizontal" group in the row for X. This group contributes the term X Y, because these are the variables that do not change in the group. The other group is a square group that wraps from the last column to the first column. In this group X and Y have different values but Z is always false, so this group contributes the term Z, and the simplified function is:
F = Z + X Y
The truth table for a function of 4 variables has 16 rows, so the kmap has 16 boxes. For 4 variables we put two variables in the rows and two variables in the columns, so there are 4 rows and 4 columns. The row and column values are ordered as they are in the kmap for a function of three variables, not as they are ordered in the truth table. This is because we want neighboring cells values to differ in only one of the variables.
The groups we form must contain either 2, 4, 8, or 16 cells. A group in the kmap can now wrap around the first and last column, first and last row, and the corners.
For 2 and 3 variables, we start with the truth table, write the Boolean expression, and then draw the kmap. Since the truth table for 4 variables is so large, we will start with the Boolean expression, and use that to create the kmap.
F = w x y z + w x y z + w x y z + w x y z + w x y z
The kmap for this function is:
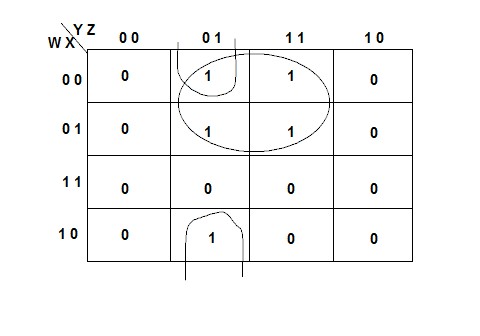
The kmap has two groups. One is the "square" group. This group contributes the term w z, because these are the variables that do not change in the group. The other group is a "horizontal" group that wraps from the last row to the first row. In this group x is false and y and z are always true, but the value of w changes. Therefore this group contributes the term x y z, and the simplified function is:
F = w z + x y z
F = w x y z + w x y z + w x y z + w x y z + w x y z + w x y z
The kmap for this function is:
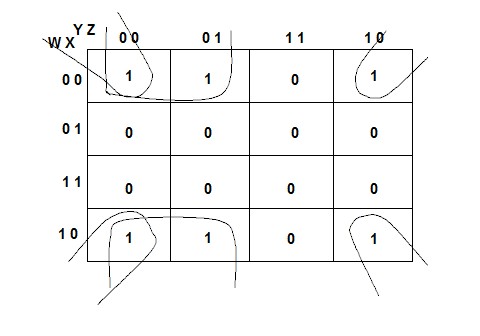
The kmap has two groups. One is the "square" group in the first two columns. This group wraps around the first row and the last row, and it contributes the term x y, because these are the variables that do not change in the group. The other group is another "square" group that includes all 4 corners. In this group x is false and z is false, but the values of w and y change. Therefore this group contributes the term x z, and the simplified function is:
F = x y + x z
Email Me |
Office Hours |
My Home Page |
Department Home |
MCC Home Page
© Copyright Emmi Schatz 2016