CSC236 Data Structures

Heaps and Heap Sort

Heaps

There are two types of heaps: minheaps and maxheaps. Both are complete binary trees.

A maxheap is a complete binary tree where, for each node, the value in the node is greater than the values in the node's children. There is no restriction on the relationship of the values in the children, like there is in a BST.

A minheap is a complete binary tree where, for each node, the value in the node is less than the values in the node's children. There is no restriction on the relationship of the values in the children, like there is in a BST.

So a heap has two requirements: the shape requirement (it must be a complete binary tree) and the ordering requirement, which is different for minheaps and maxheaps. Here are two sample heaps. Notice that the left child and right child of a node do not have to follow any rule regarding which is larger or smaller.

Maxheap

Minheap

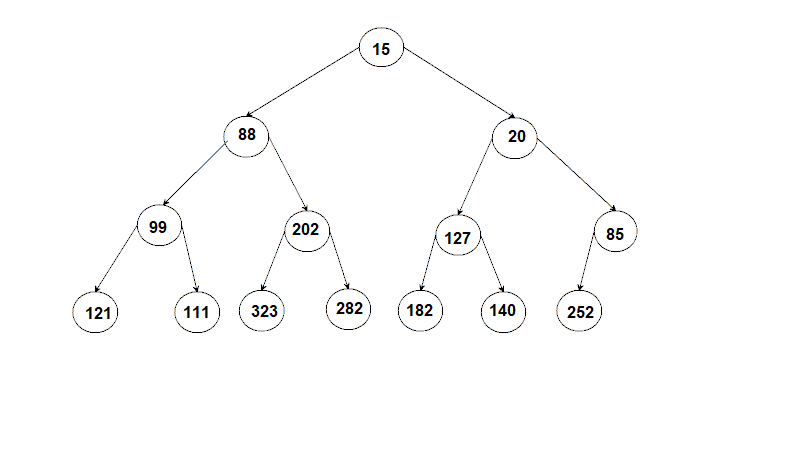
For the rest of this handout we will discuss maxheaps.

Insert

To insert into a heap, we add the new element as a new rightmost leaf. This preserves the shape needed for the heap, but the new value may violate the ordering property of the heap. If the new value is greater than the parent, we swap it with the parent, repeating until the new value is in a valid position. We call this operation "sift up".

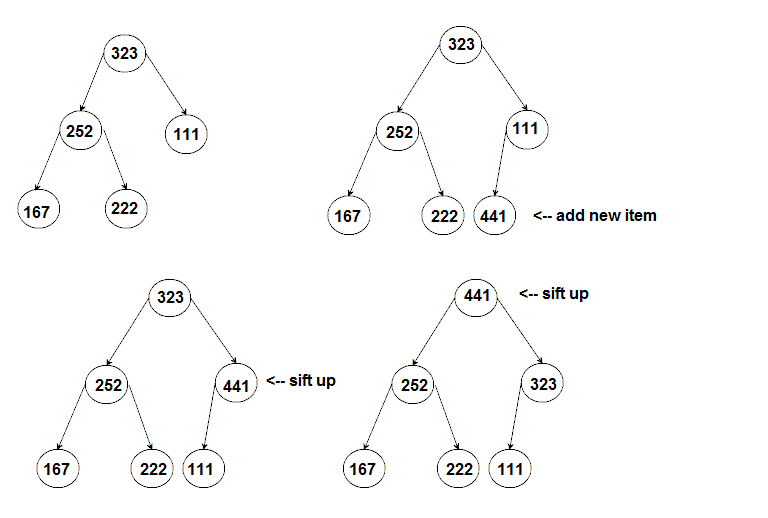
Sift up works on the path from the new node to the root. At each step we need to compare the new node and the parent, so that is one comparison at each step. In the worst case we must sift all the way up to the root, which is log(N) steps.

Delete

We delete from the root of the heap. This leaves a hole that must be filled. To preserve the heap shape, we replace the root item with the item from the rightmost leaf, and then delete that leaf. This will put a value in the root, call it v, which is too small to satisfy the heap ordering property. To correct this problem we perform "sift down" on v. In sift down we swap v with the larger of its children. This makes the root value valid, but v may still be smaller than its children, so we must repeat the sift down until v is in a valid position.

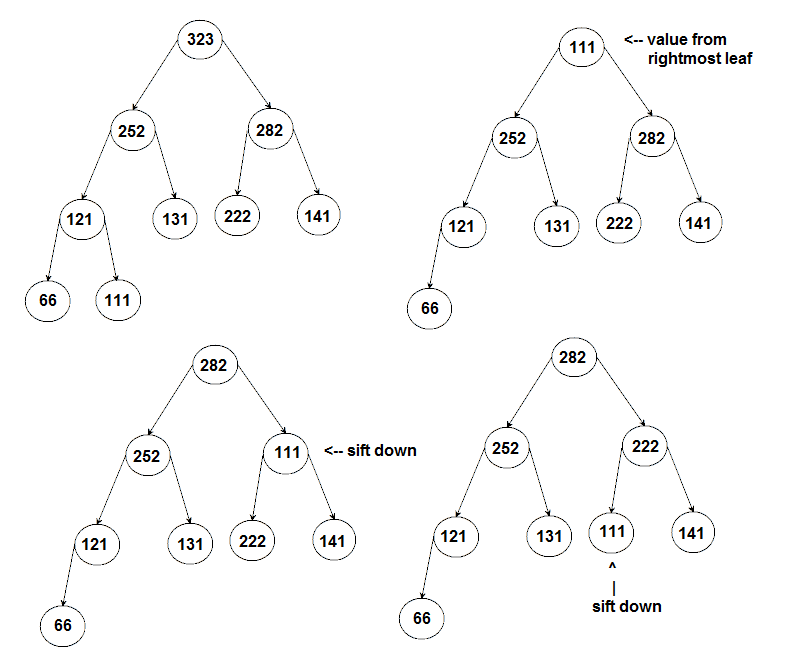
Sift down works on the path from the root to a leaf. At each stage we need to compare the children to find which is larger, and then compare the larger child to the parent. If the parent is smaller then we need to swap it with the larger child. So that is two comparisons at each step. In the worst case we must sift all the way down to a leaf, which is log N steps. Thus we see that insert and delete are both O(log N).

Storing Heap in an Array

Since the heap is a complete binary tree it is easy to store it in an array:

the root is in arr[0]
for a node in location k, the left child is in location 2k+1, the right child is in location 2k+2
the parent of the node at location k is in location (k-1)/2 (using integer division)

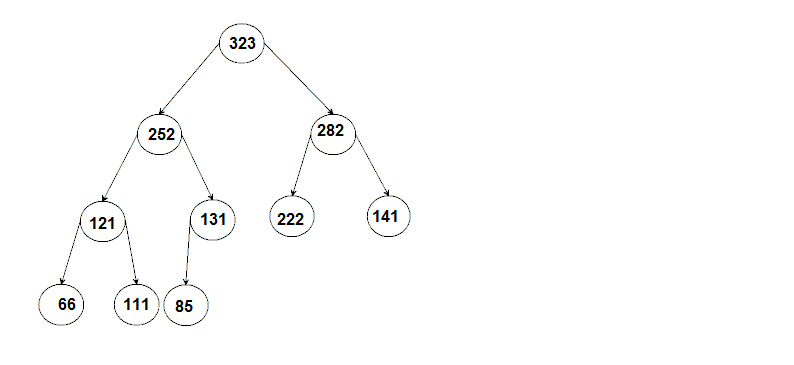
323  252  282  121  131  222  141   66  111   85
[0]  [1]  [2]  [3]  [4]  [5]  [6]  [7]  [8]  [9]

Heap Sort

Heapsort uses a maxheap in an array. The first phase builds the heap in the array. The second phase is like selection sort: each pass takes the largest (the root of the heap, in array[0]), removes it from the heap and moves it to the end of the array. After the heap is fixed up this step is repeated, removing the new root of the heap and moving it to the second-from-the-end of the array. This is repeated until the whole array is sorted.

Build Heap

The heap is built from the bottom up. The leaves are valid heaps, so the first stage is to make heaps out of the parents of the leaves, and then their parents, until the whole array has been turned into a heap. To make heaps we use the same sift down function described above. In the code below, start is the subscript of the root of the heap (the value that needs to sift down), and end is the subscript of the last element in the heap.

   siftDown(arr, start, end) {
      root = start
      while (root * 2 + 1 <= end) {
         lchild = root * 2 + 1            // subscript of left child
         swap = root
         if (arr[swap] < arr[lchild])
            swap = lchild                 // should swap root & left child
         if (lchild + 1 <= end && arr[swap] < arr[lchild+1])
            swap = lchild + 1              // should swap root & right child
         if (swap != root) {              // if one of children is greater
            swap(arr[root],arr[swap])     // swap root & larger child
            root = swap
         }
         else
            return
   }

One call to siftdown takes care of moving the root value to a valid location in one heap. To build a heap in the array we need to call it for all of the internal node positions of the heap. It can be proved that half of the nodes in a complete tree are leaves. This means that for an array of N nodes the non-leaf nodes are in array locations 0 through size/2-1. We call siftdown for each of the non-leaves, starting from the lowest non-leaves and working up to the root.

   heapify(arr, size) {
      start = size/2 - 1                   // last non leaf
      while (start >= 0) {
         siftdown(arr, start, size-1)
         start = start - 1
      }
   }

Once the heap has been built, we can sort as follows:

swap first and last (move largest to end)
fix heap: sift new root down till in valid position, cutting last element out of the heap: siftdown(arr, 0, last-1)
repeat, cutting off the last item each time

   heapsort(arr, size) {
      heapify(arr,size)
      last = size -1                       // subscript of last item
      while (last > 0) {
         swap(arr[last], arr[0])
         last = last - 1
         siftdown(arr, 0, last)
      }
   }